[最も共有された！ √] (x y)^3 identity class 9 146150

CLASSIX MATHEMATICS ASSIGNMENT2 CHAPTER – 2 POLYNOMIALS SECTIONA 1 Write the degree of the given polynomials i) ( 2x 4 )3 ii) ( t3 4 ) ( t3 9 ) 2 Write the coefficient of x4 and x in 4x3 5x4 2x2 3 3 Find the zeroes of f(z)=z2 2z 4 Find the product using suitable identities (4 5x)(45x) 5 What Transcript Example 18 Factorize 49a2 70ab 25b2 49a2 70ab 25b2 = 72 a2 70ab 52 b2 = (7a)2 70ab (5b)2 = (7a)2 (5b)2 2(7a) (5b) Using Identity (x y)2 = x2 y2 2xy where x = 7a and y = 5b = (7a 5b)2 = (7a 5b) (7a 5b) Example 18 Factorize (ii) 25/4 x2 y2/9 25/4 x2 y2/9 = 5^2/2^2 x2 y2/3^2 = (5/2 )^2 (y/3)^2 Using identity (a b) (a b) = a2 b2NCERT Class 9 Maths Lab Manual – Verify the Algebraic Identity (a – b)³ = a³ – b³ – 3ab (a – b) OBJECTIVE To verify the algebraic identity (a – b)³ = a³ – b³ – 3ab (a – b) Materials Required Geometry box Acrylic sheet Scissors Adhesive/Adhesive tape Cutter

Factorization Of Algebraic Expressions Identities Examples Cuemath

(x y)^3 identity class 9

(x y)^3 identity class 9-Here, Right hand side = Left hand side which means that (a3) (a3) is an identity Using Activity Method In this method, the algebraic identity is verified geometrically by taking different values of a x and yVolume of cuboid = I x b x h;

Class 8 Maths Chapter 9 Algebraic Expressions And Identities Merupulu

Hi everyonein this video, I tell you about " x^3y^3=(xy)(x^2xyy^2) "?channel link https//wwwyoutubecom/channel/UC7Uui8og_cIpQaH9ItVWM3Q`````CBSE Class 9 Maths Lab Manual – Algebraic Identity (a 3 b 3) = (a b) (a 2 – ab b 2) Objective To verify the identity a 3 b 3 = (a b) (a 2 – ab b 2) geometrically by using sets of unit cubes Prerequisite Knowledge Volume of cube = (edge) 3;State whether the following statements are true or false Give reasons to justify your answers (a) The degree of polynomial 5 x5 6 x4 8 x2 is 4 (b) The algebraic expression is a polynomial (c) The polynomial is a quadratic trinomial Using the long division method, determine the remainder when the polynomial 4 x5 2 x4 x3 4 x2 7

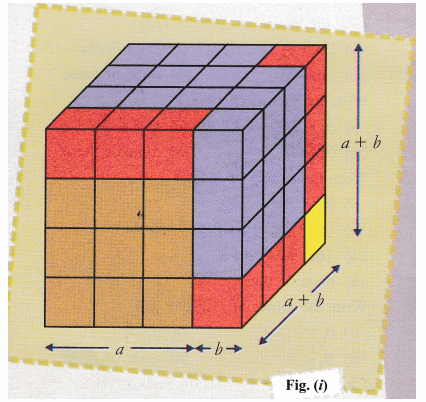
NCERT Class 9 Maths Lab Manual – Verify the Algebraic Identity (ab)³ = a³b³ 3a²b 3ab² OBJECTIVE To verify the algebraic identity (ab)³ = a³b³ 3a²b 3ab² Materials Required Acrylic sheets Adhesive/Adhesive tape Scissors Geometry Box Cutter Prerequisite Knowledge Concept of cuboid and its volume Concept of cube and its volume Theory CuboidDon't stop learning now Participate in the Scholorship Test for FirstSteptoDSA Course for Class 9 to 12 students My Personal Notes arrow_drop_upCBSE Class 9 Maths Lab Manual – Algebraic Identity (a – b) 2 = a 2 – 2ab b 2 Objective To verify the identity (a – b) 2 = (a 2 – 2ab b 2) by paper cutting and pasting Prerequisite Knowledge Area of a square = (side) 2 Area of a rectangle = l x b Materials Required A white sheet of paper, glazed papers, a pair of scissors

 Ex 25, 11 Factorise 27 𝑥﷮3﷯ 𝑦﷮3﷯ 𝑧﷮3﷯ – 9xyz 27 𝑥﷮3﷯ 𝑦﷮3﷯ 𝑧﷮3﷯ – 9𝑥𝑦𝑧 = 3𝑥﷯﷮3﷯ 𝑦﷯﷮3﷯ 𝑧﷯﷮3﷯−9𝑥𝑦𝑧 = 3𝑥﷯﷮3﷯ Solution (3x– 4y) 3 is of the form Identity VII where a = 3x and b = 4y So we have, (3x – 4y) 3 = (3x) 3 – (4y) 3 – 3(3x)(4y)(3x – 4y) = 27x 3 – 64y 3 – 108x 2 y 144xy 2 Example 5 Factorize (x 3 8y 3 27z 3 – 18xyz) using standard algebraic identities Solution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity Use the identity (x a) (x b) = x 2 (a b) x ab to find the following = x 2 y 2 z 2 – 6xyz 8 Question 3 Find the following squares by using the identities (i Attention reader!

Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities

Expand 1 X Y 3 Whole Cube Studyrankersonline

Hello Students in this video we are going to discuss our new excercise in Class 9 NCERT Maths polynomials chapter, We have already discussed till now Remaind Ex 25, 1Use suitable identities to find the following products(i) (x 4) (x 10)(x 4) (x 10)Using (x a) (x b) = x2 (a b) x ab,Materials Required A set of 56 cubes each has dimensions (1 x 1 x 1) cubic unit

Algebraic Identities Standard Algebraic Identities Definition Examples

1

Students can download RD Sharma Class 9 Maths Chapter 4 exercise 44 PDF from below link Chapter 4 Algebraic Identities Rd Sharma Class 9 Solutions Maths Chapter 1 Number System Rd Sharma Class 9 Solutions Maths Chapter 2 Exponents Of Real Numbers Rd Sharma Class 9 Solutions Maths Chapter 3 RationalisationPolynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2 This video shows how to evaluate using the identity '(xy)3=x3y33x2y3xy2'To view more Educational content, please visit https//wwwyoutubecom/appuserie

All Identities Of Class 9 Maths Ch 2 Polynomial Brainly In

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf

The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3Phone support is available MondayFriday, 900AM1000PM ET You may speak with a member of our customer support team by calling End of Conversation Have a great day! Therefore, by using the identity (xy) 2 = x 22xyy 2 p 2 –10p25 = (p5) 2 (iii) 25m 2 30m9 Ans Given 25m 2 30m9 Since, 25m 2 , 30m and 9 can be substituted by (5m) 2, 2×5m×3 and 3 2 respectively we get, = (5m) 2 2×5m×3 3 2 Therefore, by using the identity (xy) 2 = x 2 2xyy 2 25m 2 30m9 = (5m3) 2 (iv) 49y 2 84yz36z 2 Ans Given 49y 2

Ncert Solutions For Class 8 Maths Algebraic Expressions And Identities Ex 9 4 Algebraic Expressions Math Class 8

Class 8 Maths Chapter 9 Algebraic Expressions And Identities Merupulu

= (x y)(x 2 y 2 2xy x 2 xy y 2) using identity, (a b) 2 = a 2 b 2 2 ab) = (x y) (3xy) Hence, one of the factor of given polynomial is 3xy Question 18 The coefficient of x in the expansion of (x 3) 3 is (a) 1 (b) 9 (c) 18 (d) 27 Solution (d) Now, (x 3) 3 = x 3 3 3 3x (3)(x 3) using identity, (a b) 3 = a 3 b 3Rs Aggarwal 19 Solutions for Class 9 Math Chapter 3 Factorisation Of Polynomials are provided here with simple stepbystep explanations These solutions for Factorisation Of Polynomials are extremely popular among Class 9 students for Math Factorisation Of Polynomials Solutions come handy for quickly completing your homework and preparing for examsWe shall use the identity xy x y = x 2y 2 Here By applying in identity we get Hence the value of is (iv) The given expression is We have So we can express and in the terms of 100 as We shall use the identity xy x y = x 2y 2 Here By applying in identity

Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Cbsetuts Com

Algebraic Identities Of Polynomials A Plus Topper

 Evaluate the following using suitable identities (i) (99) 3 (ii) (102) 3 (iii) (998) 3 Solution (i) (99) 3 = (100 – 1) 3 Identity (x – y) 3 = x 3 – y 3Ex 25 Class 9 Maths Question 12 Verify that x 3 y 3 z 33xyz = (x y z)(x y) 2 (yz) 2 (zx) 2 Solution We have, x 3 y 3 z 3 – 3xyz = (x y z) x 2 y 2 z 2 – xy – yz – zx = (x y z)2x 2 2y 2 2z 22xy2yz 2zx = (x y z)x 2 x 2 y 2 y 2 z 2 z 22xy2yz2zx = (x y z)x 2 y 2 – 2xy y(i) To prove x 3 y 3 = (x y) (x 2 – xy y 2) Now, using identity VI we can say (x y) 3 = x 3 y 3 3xy (xy) Or, (xy) 3 – 3xy (x y) = x 3 y 3

Chapter 4 Algebraic Identities Rd Sharma Solutions For Class 9 Mathematics Cbse Topperlearning

Standard Identities Of Binomials And Trinomials Equations Examples

For today's students, learning can happen anytime, anywhere Our mission is to improve 6th to 10th outcomes for all students and make learning more intuitive, more interesting, more personalised and more affordableUsing the above identity, the equation x 6 − y 6 can be factorised as follows x 6 Class 9 Maths Chapter 3 Unit 2 163 Qs > Related questions Factorize the following expression 8 x 3Class IX Repair parts and components to include kits, assemblies, and subassemblies (repairable or nonrepairable) required for maintenance support of all equipment Class X Material to support nonmilitary programs such as agriculture and economic development (not included in Classes I through IX)

Algebra Formula Solved Examples List Of Algebraic Formulas

Factorization Of Algebraic Expressions Identities Examples Cuemath

 Polynomials Class 9 Extra Questions Very Short Answer Type Question 1 Factorise 125x 3 – 64y 3 Solution 125x 3 – 6443 = (5x) 3 – (4y) 3 By using a3 – b3 = (a – b) (a 2 ab b 2), we obtain 125x 3 – 64y 3 = (5x – 4y) (25x 2 xy 16y 2) Question 2 Find the value of (x y) 2 (x – y) 2 Solution (x y) 2 (x – y) 2 = x 2 y 2 2xy x 2 y 2 – 2xy Since x − y = 3 xy=3 x − y = 3 implies y = x − 3, y=x3, y = x − 3, substituting this into the given identity gives a x (x − 3) b x c (x − 3) 9 = 0 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 \begin{aligned} ax(x3)bxc(x3)9&=0\\ ax^2(3abc)x3(c3)&=0 \end{aligned} a x (x − 3) b x c (x − 3) 9 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 = 0 9 (x y) 3 = x 3 y 3 3xy (x y) = x 3 3x 2 y 3xy 2 y 3 10 (x y) 3 = x 3 y 3 3xy (x y) = x 3 3x 2 y 3xy 2 y 3 11 x 3 y 3 z 3 3xyz = (x y z) (x 2 y 2 z 2 xy yz zx) 12 x 2 y 2 = ½ (x y) 2 (x – y) 2 13 xy = ¼ (x y) 2 (x – y) 2 14 x 2 y 2 = (x y

Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials

X Y 3 Formula Class 9 Novocom Top

Problem Solve (x 3) (x – 3) using algebraic identities Solution By the algebraic identity, x 2 – y 2 = (x y) (x – y), we can write the given expression as;By using standard formulae, expand the following (1 to 9) 1 (i) (2x 7y) 2 (ii) (1/2 x 2/3 y) 2 Solution (i) (2x 7y) 2 It can be written as = (2x) 2 2 × 2x × 7y (7y) 2 So we get = 4x 2 28xy 49y 2 (ii) (1/2 x 2/3 y) 2 It can be written as = (1/2 x) 2 2 × ½x 2/3y (2/3 y) 2 So we get = ¼ x 2 2/3 xy 4/9 y 2 2 (i) (3x 1/2x) 2 (ii) (3x 2 y 5z) 2Algebraic Identities Cubic Type ,Polynomials Get topics notes, Online test, Video lectures, Doubts and Solutions for CBSE Class 9 on TopperLearning

Revision Notes For Maths Chapter 2 Polynomials Class 9th Askiitians

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com

 CBSE Class 9 Maths Lab Manual – Algebraic Identity (a b) 3 = a 3 b 3 3a 2 b 3ab 2 Objective To verify the identity (ab) 3 = a 3 b 3 3a 2 b 3ab 2 geometrically by using sets of unit cubes Prerequisite Knowledge Volume of a cube = (edge) 3 Volume of a cuboid = l x b x h Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) Ex 25, 9 Verify (ii) x3 y3 = (x y) (x2 xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x yClass 9 RD Sharma Solutions Chapter 4 Algebraic Identities Ex 43 Question 1 Find the cube of each of the following binomial expressions Solution Question 2 If a b = 10 and ab = 21, find the value of a 3 b 3 Solution a b = 10, ab = 21

Write The Following Cubes In Expanded Form Cbse Class 9 Maths Learn Cbse Forum

Factorisation Rs Aggarwal Class 8 Maths Solutions Ex 7a Quadratics Maths Solutions Quadratic Equation

 Transcript Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence provedThis video shows how to evaluate using the identity '(xy)3=x3y33x2y3xy2' To view more Educational content, please visit https//wwwyoutubecom/appuseriSelina Concise Mathematics Part I Solutions for Class 9 Mathematics ICSE, 5 Factorisation All the solutions of Factorisation Mathematics explained in detail by experts to help students prepare for their ICSE exams

Class 8 Maths Chapter 9 Algebraic Expressions And Identities Merupulu

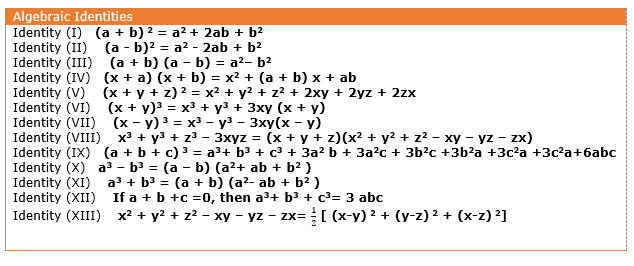
All Useful Algebraic Identities With Proof Examples Physicscatalyst S Blog

Class 9 Maths Polynomials Algebraic Identities Algebraic Identities Algebraic identity is an algebraic equation that is true for all values of the variables occurring in it ( x y) 2 = x2 2 xy y2 ( x – y) 2 = x2 – 2 xy y2 x2 – y2 = ( x y) ( x – y) ( x a) ( x b) = x2 ( a b) x ab (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zxNCERT Class 9 Maths Lab Manual – Verify the Algebraic Identity (ab)² = a² 2abb² OBJECTIVE To verify the algebraic identity (ab)² = a² 2abb² Materials Required Drawing sheet Pencil Cellotape Coloured papers Cutter Ruler Prerequisite Knowledge Square and its area Rectangle and its area Theory A square is a quadrilateral whose allAlgebraic Identities Polynomials, Class 9, Mathematics EduRev Notes is made by best teachers of Class 9 This document is highly rated by Class 9

Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8

Factorisation Using Identities Factoring Algebraic Expressions Examples

 In the 4th chapter of Class 9 RD Sharma Solutions students will study important identities as listed below Algebraic Identities Introduction Identity for the square of a trinomial Sum and difference of cubes Identity These books are widely used by the students who wish to score high in board exams(9) Verify (i) x 3 y 3 = (x y) (x 2 − xy y 2) (ii) x 3 – y 3 = (x − y) (x 2 xy y 2) using some nonzero positive integers and check by actual multiplication Can you call these as identites ?We already have an identity for (x y) 3 So, let's try to derive the identity x 3 y 3 using the identity for (x y) 3 Let's first try to understand this geometrically Let's join our cubes as shown above We arranged both cubes in such a way to convert it into a cube as shown above

Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers

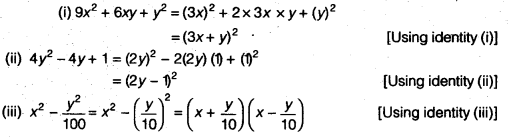
Polynomials Maths Class 9 Ncert Solutions Getstudysolution Com

(x 3) (x – 3) = x 2 – 3 2 = x 2 – 9 Problem Solve (x 5) 3 using algebraic identities Solution We know, (x y) 3 = x 3 y 3 3xy(xy) Therefore, (x 5) 3 = x 3 5 3 3x5(x5)

Pearson Maths Class 9 Solution Pages 1 50 Flip Pdf Download Fliphtml5

Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

Rd Sharma Class 9 Chapter 4 Algebraic Identities

X 3 Y 3 Proof A 3 B 3 Formula Proof Youtube

Gyanpub Learning Polynomials Class 9 Extra Questions Maths Chapter

Rd Sharma Class 9 Solutions Algebraic Identities Exercise 4 3 8 Rdsharmaclass9 Class9solutions Rdsharmaclass9solutions Rd Math Notes Solutions Class

Cbse Class 8 Mathematics Algebraic Identities Bridge Course Worksheet

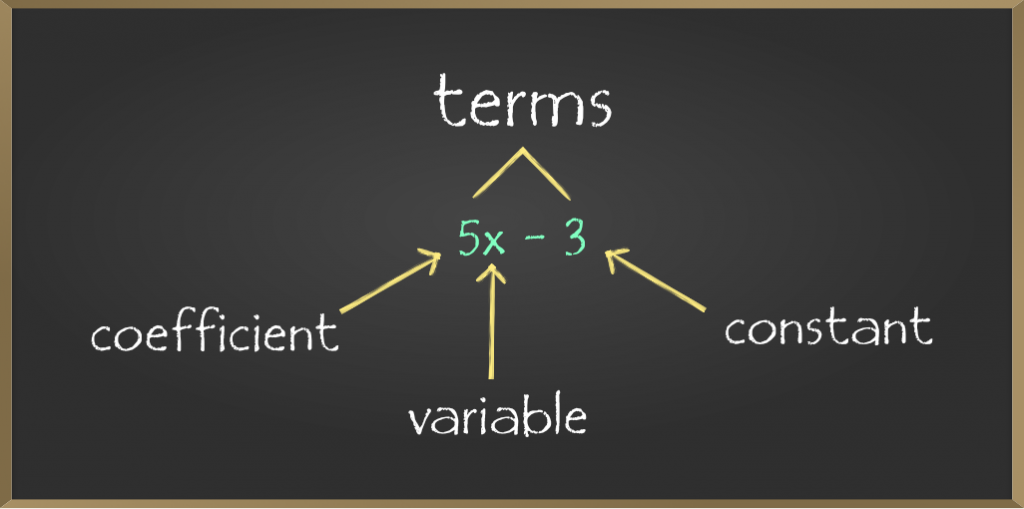
Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks

Standard Identities Of Binomials And Trinomials Equations Examples

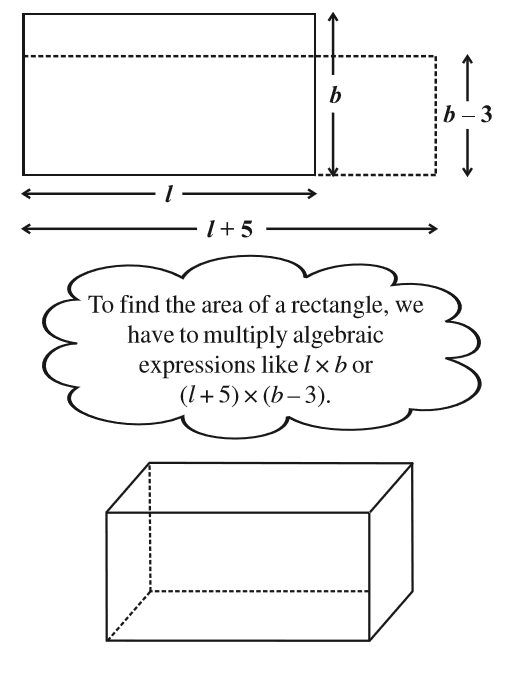
Algebraic Expressions And Identities Ncert Class 8 Maths

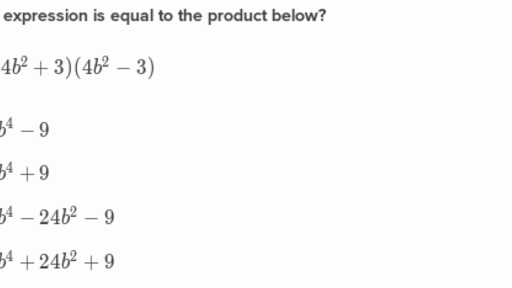
Algebraic Expressions Class 9 Foundation Math Khan Academy

Algebra Formulas List Of Important Algebraic Expressions Formulas

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5

Algebraic Expressions And Identities

Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks

Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

Factorization Of Cubic Polynomials Important Questions Class 9 Polynomials Class 9 Ex 2 5 Q9 Youtube

3

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5 Studyrankersonline

Algebraic Identities Of Polynomials A Plus Topper

Standard Identities Of Binomials And Trinomials Equations Examples

5 Extra Questions For Class 9 Maths Chapter 2 With Solution Polynomials Zeroes Remainder Theorem Factorization And Algebraic Identities

Use Suitable Identities To Find The Following Products I X 4 X 10 Ii X 8 X 10 Ii Youtube

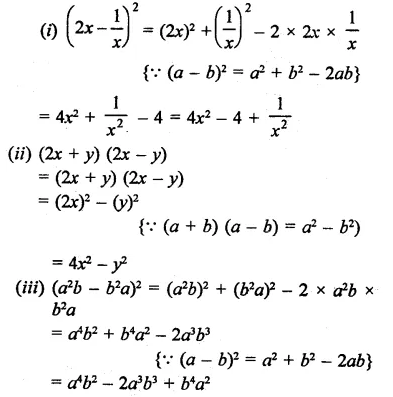
Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4 1

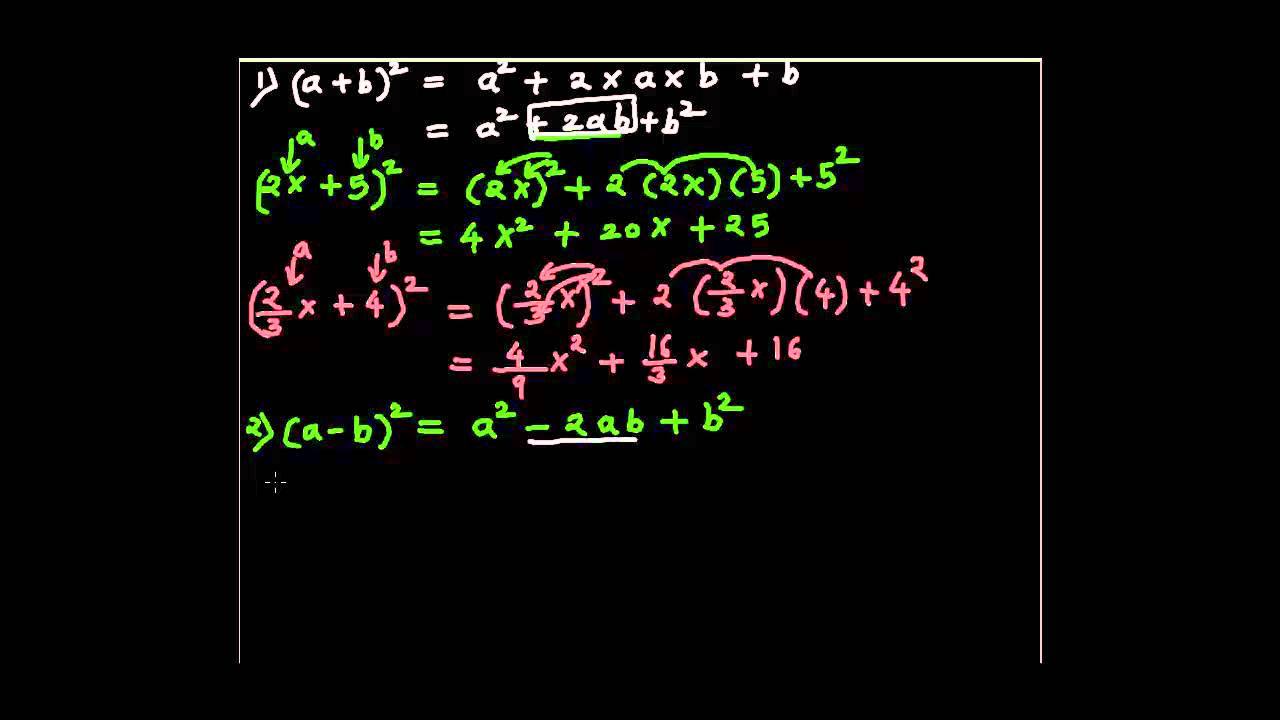
Factorization Using Identities

Ncert Solutions For Class 9 Maths Exercise 2 5 Chapter 2 Polynomials Study Path

Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities In Hindi

Rd Sharma Class 9 Chapter 4 Algebraic Identities

Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8

X Y 3 Identity Class 9 Novocom Top

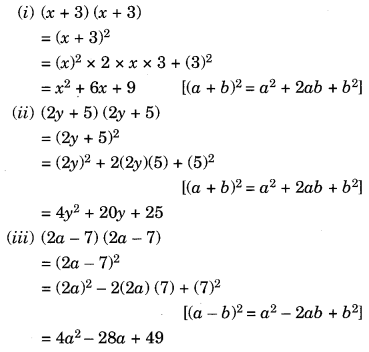
Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Learn Cbse

How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In

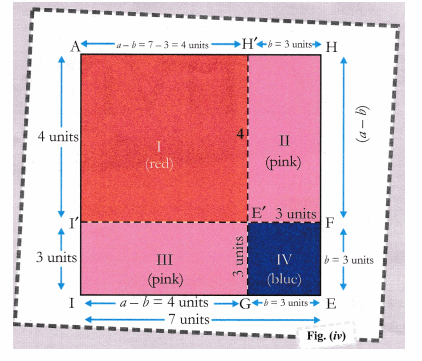
Cbse Class 9 Maths Lab Manual Algebraic Identity A B 2 2ab B2 Cbse Sample Papers

1 9m02 4 Cv1 ब ज य सर वसम क V Alegebraic Identity V Youtube

What Is The Answer Of X Y Quora

X Y 3 Identity Class 9 Novocom Top

Polynomials Important Questions Of Identities Algebraic Identities Class 9 Oda Class Youtube

If Math X Y 3 Math And Math X 2 Y 2 3 Math Then What Is The Value Of Math X 2 Y 2 Math Quora

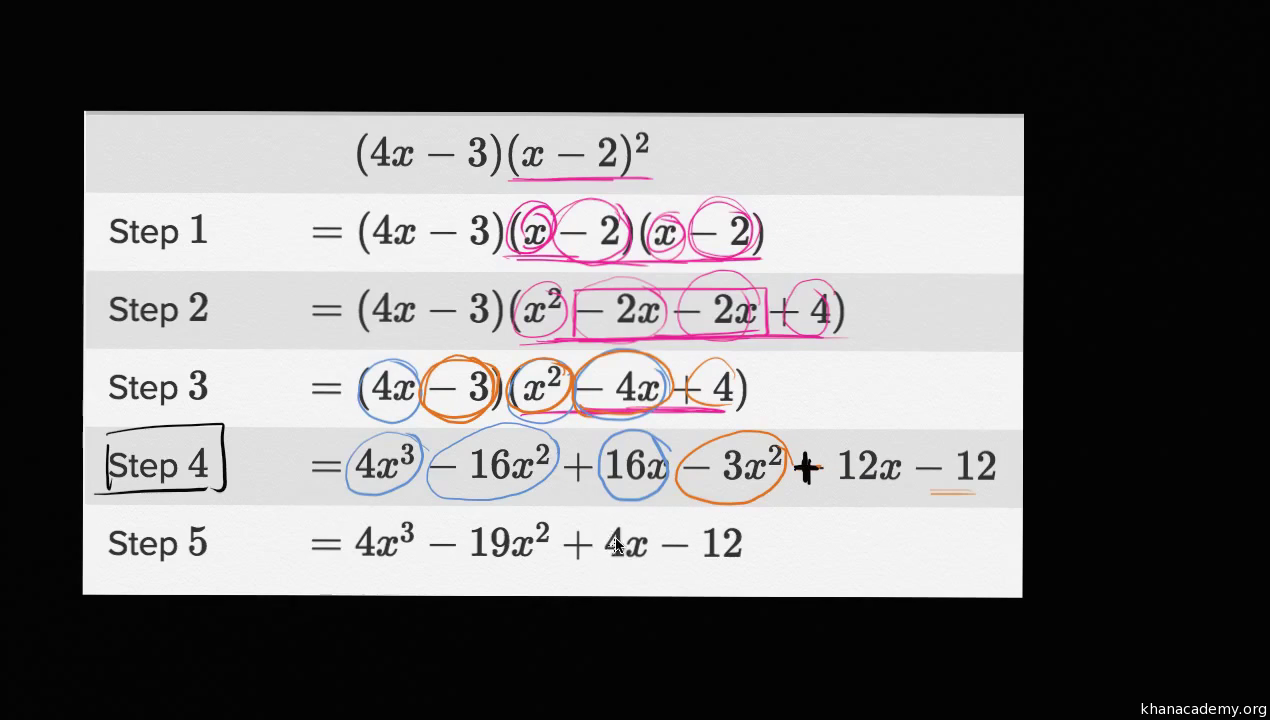
Analyzing Polynomial Identities Video Khan Academy

Expanding Algebraic Expressions Using Identities Worksheets

Algebra Formulas For Class 9 Pdf Download Free Here

Exercise 25 Question 1 Use Suitable Identities To Find The Following Products X 4 X 10x 8x 10 I 3 3 3x 43x 5 Iii 2 Iv 3 2x 3 2x V Answer I By Using The Identity X Ax B X A B

Ex 2 5 9 Verify I X3 Y3 X Y X2 Xy Y2 Ex 2 5

Algebraic Identities Of Polynomials A Plus Topper

Pearson Maths Class 9 Solution Pages 1 50 Flip Pdf Download Fliphtml5

Dcmc Math Class 8 17

Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube

Algebraic Identities Of Polynomials A Plus Topper

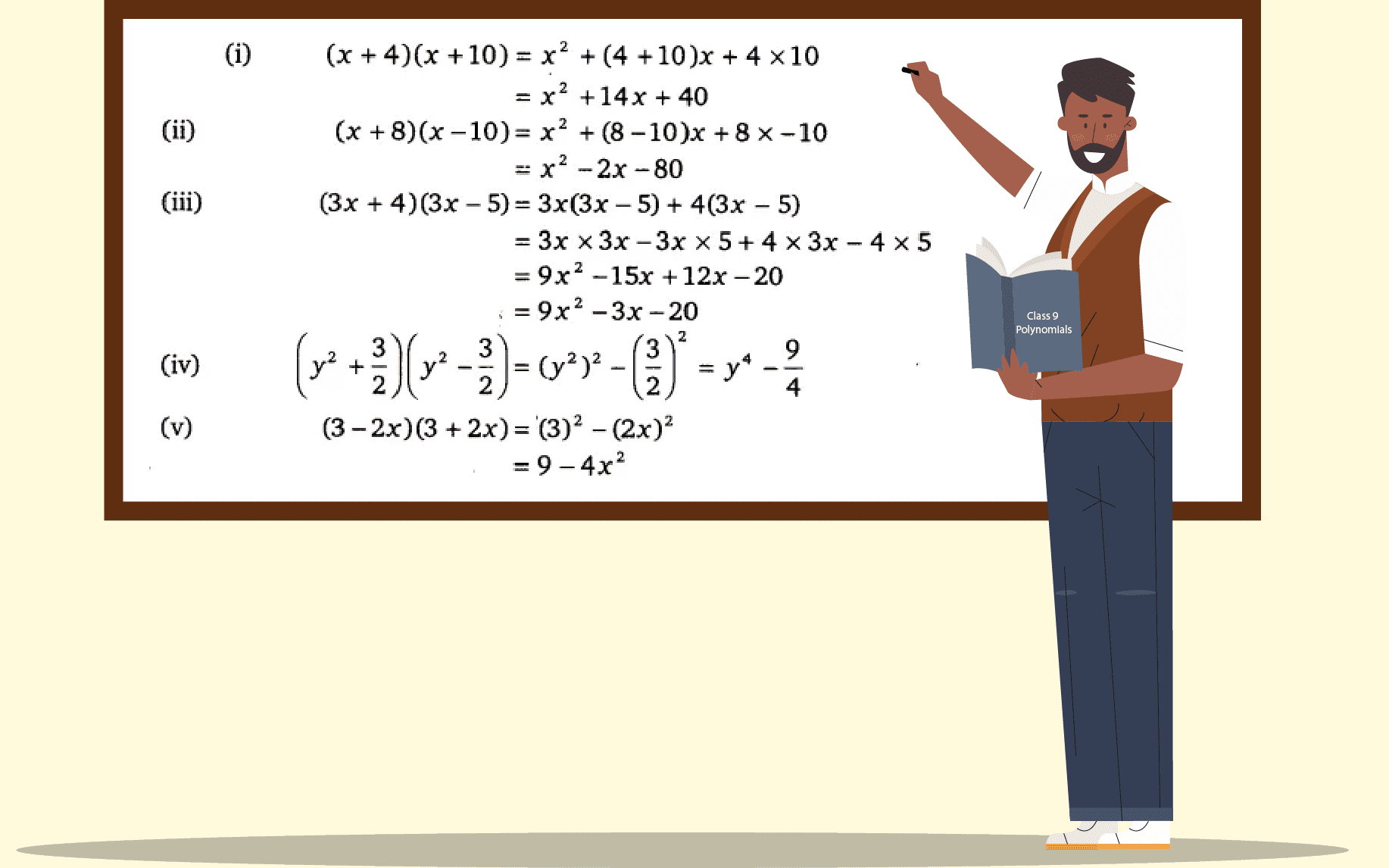
Class 9 Polynomials Study Notes And Important Questions Leverage Edu

X Y 3 Identity Class 9 Novocom Top

Kpk 9th Maths Ch01 Pdf Matrix Mathematics Algebra

Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 5 Access Free Pdf

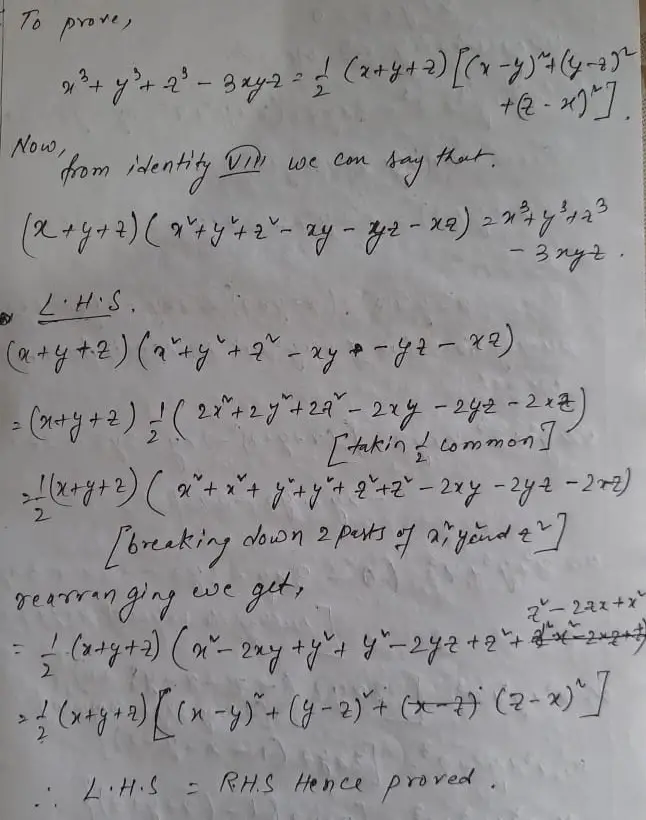
Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5

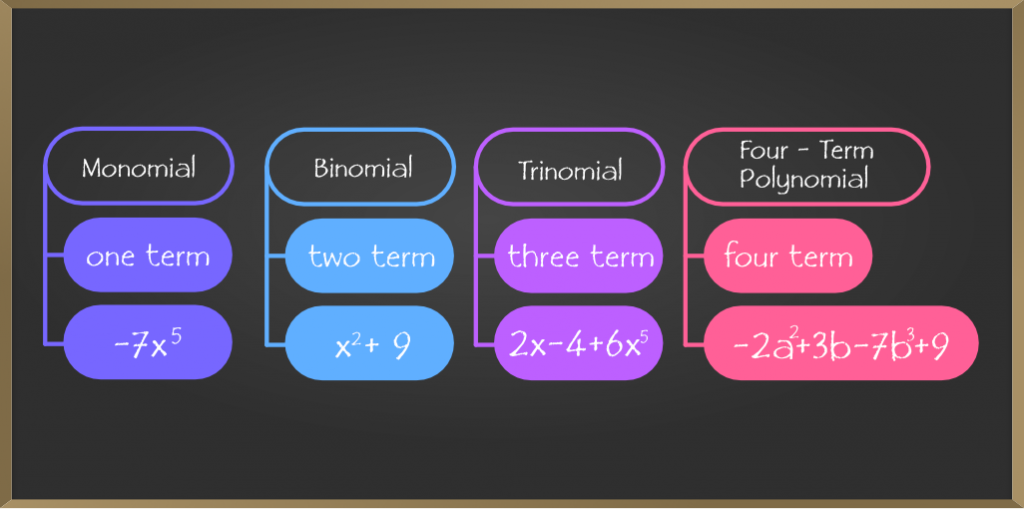
Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks

Cbse Class 9 Algebraic Identities Offered By Unacademy

1

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

Questions On Algebraic Expressions Algebraic Identities Algebraic Formulas

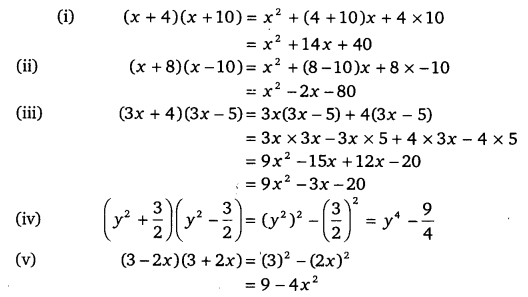
Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com

Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks

Rd Sharma Class 9 Solutions Algebraic Identities Exercise Flickr

What Are The Factors Of X Y 3 X3 Y3 Brainly In

Ex 4 3 Q17 Find The Value Of 27x 3 8y 3 If I 3x 2y 14 And Xy 8 Ii 3x 2y

If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9

Expanding Algebraic Expressions Using Identities Worksheets

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf

Algebraic Expressions Definition Types Formulas

Rd Sharma Solutions Class 9 Factorization Of Algebraic Expressions Ex Pdf Free Download

How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com

Example 11 Using The Identity I Find I 2x 3y 2 Ii 103 2

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5

Ex 9 5 3 Find The Squares By Using Identities I B 7 2

Identity Mathematics Wikipedia

Poster Algebraic Identities Chart